ITU ACM Contest 1 Solutions
Posted on 12 August, 2018 in Algorithm
Hello there,
We are going to analyze each question from ITU ACM Contest 1. You can check the questions from this link.
Question One - Bekci and His Machine Learning Experience - O(N•M)
Int this question. We need to do following;
1- Fill the static Fibonacci Numbers array. Until 80 is enough for this question.
2- For each minimum number we can use binary search for finding the closest.
#include <cmath>
#include <cstdio>
#include <utility>
#include <vector>
#include <iostream>
#include <climits>
#include <limits>
#include <algorithm>
#include <iostream>
#include <set>
#include <fstream>
#include <queue>
#include <bitset>
#include <map>
#include <stack>
#define ll long long
using namespace std;
int main() {
// We need to fill our fibVector array with fib numbers. Fibonacci 80 is big enough.
vector<ll> fibVector(80);
fibVector[1] = 1, fibVector[2] = 1;
for (int i=3; i<80; i++) {
fibVector[i] = fibVector[i-1] + fibVector[i-2];
}
int n,m;
cin >> n >> m;
// We need to find minimum value for each row.
vector<ll> smallestArray(static_cast<unsigned long>(n));
ll readVal;
for(int i=0;i<n;i++){
ll minVal = LONG_LONG_MAX;
for(int j=0;j<m;j++){
scanf("%lld", &readVal);
minVal = min(minVal, readVal);
}
smallestArray[i] = (minVal);
}
// We can use binary search for finding the closest item in the fibVector
for (ll &e : smallestArray) {
ll indexOfIt = (upper_bound(fibVector.begin(), fibVector.end(), e) - fibVector.begin()) - 1;
if(fibVector[indexOfIt+1] - e <= e - fibVector[indexOfIt]) e = fibVector[indexOfIt+1];
else e = fibVector[indexOfIt];
if(e == 0) e = 1;
}
// Printing the matrix.
for(ll i=0;i<n;i++){
for(ll j=0;j<m;j++){
printf("%lld ", smallestArray[i]);
}
printf("\n");
}
return 0;
}
Question Two - Party Boy Halil - - O(N•M)
This question is a little bit tricky. We need to do following for solving this question.
1 - Assign a distinct number to each available spot.
1 - Mark every single available slot with either 1 or 0.
2 - Specify roads that we can take for each 0 marked spot. We have a bipartite graph now.
3 - Apply the Ford-Fulkerson Maximum Flow Algorithm to the bipartite graph.
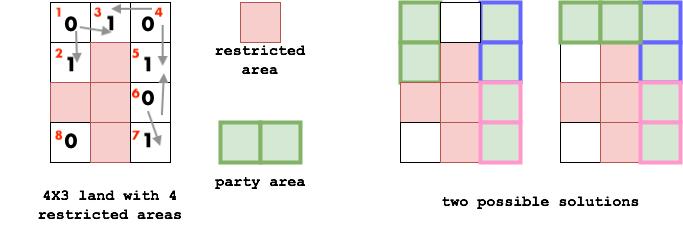
Figure 1: Creating the bipartite graph.
#include <cmath>
#include <cstdio>
#include <utility>
#include <vector>
#include <iostream>
#include <climits>
#include <limits>
#include <algorithm>
#include <iostream>
#include <set>
#include <fstream>
#include <queue>
#include <bitset>
#include <map>
#include <stack>
using namespace std;
vector<vector<int>> roads;
vector<vector<pair<int,int>>> colors;
vector<int> zeros;
vector<int> ones;
int counter;
int V;
struct node{
int x,y,leftOrRight,counter;
}tempNode;
void graphCreator(pair<int, int> currentNode, vector<vector<int>> &land){
int movements[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
queue<node> q;
tempNode.leftOrRight = 0, tempNode.x = currentNode.first, tempNode.y = currentNode.second,tempNode.counter = ++counter;
colors[tempNode.x][tempNode.y] = make_pair(tempNode.leftOrRight,tempNode.counter);
q.push(tempNode);
land[tempNode.x][tempNode.y] = 1;
while(!q.empty()){
node cNode = q.front(); q.pop();
if(cNode.leftOrRight == 0) zeros.push_back(cNode.counter);
else ones.push_back(cNode.counter);
for (auto &movement : movements) {
int currX = cNode.x + movement[0];
int currY = cNode.y + movement[1];
if(currX>=0 && currX<land.size() && currY>=0 && currY<land[0].size() && land[currX][currY] == 0){
node tempOne{};
land[currX][currY] = 1;
tempOne.x = currX, tempOne.y = currY, tempOne.leftOrRight = (cNode.leftOrRight+1)%2, tempOne.counter = ++counter;
colors[tempOne.x][tempOne.y] = make_pair(tempOne.leftOrRight, tempOne.counter);
if(cNode.leftOrRight == 0)
roads[cNode.counter].push_back(tempOne.counter);
else
roads[tempOne.counter].push_back(cNode.counter);
q.push(tempOne);
}else if (currX>=0 && currX<land.size() && currY>=0 && currY<land[0].size() && land[currX][currY] == 1 && colors[currX][currY].first != -1){
if(cNode.leftOrRight != colors[currX][currY].first) {
if (cNode.leftOrRight == 0)
roads[cNode.counter].push_back(colors[currX][currY].second);
else
roads[colors[currX][currY].second].push_back(cNode.counter);
}
}
}
}
}
bool routeFinder(vector<vector<int>> rGraph, int s, int t, vector<int> &parent) {
vector<bool> visited(rGraph.size(), false);
queue <int> q;
q.push(s);
visited[s] = true;
while (!q.empty()) {
int u = q.front();
q.pop();
for (int v=0; v<rGraph[u].size(); v++) {
if (!visited[rGraph[u][v]]) {
q.push(rGraph[u][v]);
parent[rGraph[u][v]] = u;
visited[rGraph[u][v]] = true;
}
}
}
return visited[t];
}
int fordFulkerson(int s, int t) {
int v;
vector<vector<int>> rGraph = roads;
vector<int> parent(V, 0);
int max_flow = 0;
while (routeFinder(rGraph, s, t, parent)) {
for (v=t; v != s; v=parent[v]) {
rGraph[parent[v]].erase(remove(rGraph[parent[v]].begin(), rGraph[parent[v]].end(), v), rGraph[parent[v]].end());
rGraph[v].push_back(parent[v]);
}
max_flow++;
}
return max_flow;
}
int main() {
int t;
cin >> t;
int n, m, k;
while(t-- > 0){
cin >> n >> m;
zeros.clear(), ones.clear(), roads.clear();
counter = 0;
cin >> k;
vector<vector<int>> land(n, vector<int>(m,0));
vector<pair<int,int>> rLocations(k);
// Reading the input and marking restricted areas as 1.
for(int i=0;i<k;i++) cin >> rLocations[i].first >> rLocations[i].second;
for(auto p: rLocations) land[p.first-1][p.second-1] = 1;
// V means how many available slots that we have
V = (n*m)-k+2;
roads.resize(V);
colors.resize(n);
for(int i=0;i<n;i++) colors[i].resize(m);
for(int i=0;i<n;i++) for(int j=0;j<m;j++) colors[i][j] = make_pair(-1,0);
// Doing the marking with 0 or 1.
for(int i=0;i<n;i++) for(int j=0;j<m;j++) if(land[i][j] == 0) graphCreator(make_pair(i, j), land);
// Creating the bipartite graph which is called as roads.
for (int zero : zeros) roads[0].push_back(zero);
for (int one : ones) roads[one].push_back(V-1);
// Running Ford-Fulkerson algorithm.
cout << fordFulkerson(0,V-1) << endl;
}
return 0;
}
Question Three - Yavuz and His Brilliant 3ncrypt10n Technique - O(N•Di)
We need to use a trie data structure in this question.
1 - Create a trie with the words of d!ct10n4ry.
2 - Search every word in the sentence in the trie.
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int MAXC = 300;
const int MAXL = 3003;
struct Node{
char val;
bool isRoot, isEnd;
Node *parent;
Node *children[MAXC];
};
int N, M, L;
char ar[MAXL];
void add( Node *p, int ind ){
if( ind == L ){
p->isEnd = true;
return;
}
int go = (int)(ar[ind]);
if( !p->children[go] ){
p->children[go] = new Node;
p->children[go]->isRoot = false;
p->children[go]->val = ar[ind];
p->children[go]->isEnd = false;
p->children[go]->parent = p;
}
add(p->children[go], ind+1);
}
void write(Node *p){
if (p->isRoot)
return;
write(p->parent);
printf("%c", p->val);
}
Node *search( Node *p, int ind ){
if( p->isEnd )
return p;
if( ind == L )
return NULL;
int go = (int)ar[ind];
if (!p->children[go])
return NULL;
return search(p->children[go], ind+1);
}
int main(){
scanf("%d%d", &M, &N);
// Creating the root of the trie data structure
Node *root;
root = new Node;
root->isRoot = true;
root->isEnd = false;
// Adding the strings one by one to the trie
for( int i=0 ; i<N ; i++ ){
scanf("%s", ar);
L = strlen(ar);
add(root, 0);
}
// If we can find the string in the trie, we need to change it.
for( int i=0 ; i<M ; i++ ){
scanf("%s", ar);
L = strlen(ar);
Node *p = search(root, 0);
if(!p)
printf("%s", ar);
else
write(p);
if( i != M-1 )
printf(" ");
}
puts("");
return 0;
}
Special thanks to Burak Bugrul for the implementation of this question.
Question Four - Oğuz and His New Job - O(N)
The question is asking for the how many blocks that we can fill with rainwater. After calculating this we can simply multiply it with M and K.
We need to do the following for calculating the rainwater blocks.
1 - Find the left blockers of each index.
2 - Find the right blockers of each index.
3 - Calculate the fillable volume by using right blockers and left blockers.
#include <cmath>
#include <cstdio>
#include <utility>
#include <vector>
#include <iostream>
#include <climits>
#include <limits>
#include <algorithm>
#include <iostream>
#include <set>
#include <fstream>
#include <queue>
#include <bitset>
#include <map>
#include <stack>
using namespace std;
const int MAXN = 1e6+16;
int N;
int ar[MAXN];
int L[MAXN];
int R[MAXN];
long long int M, K, res;
int main(){
scanf("%d%lld%lld", &N, &M, &K);
for( int i=1 ; i<=N ; i++ ) scanf("%d", ar+i);
// Finding the left blockers
for( int i=1 ; i<=N ; i++ ){
L[i] = L[i-1];
if( ar[i] > ar[i-1] && ar[i] > ar[i+1] )
L[i] = max(L[i], ar[i]);
}
// Finding the right blockers
for( int i=N ; i > 1 ; i-- ){
R[i] = R[i+1];
if (ar[i] > ar[i - 1] && ar[i] > ar[i + 1])
R[i] = max(R[i], ar[i]);
}
// Calculating the how much rain water that the index can get.
for( int i=2 ; i<N ; i++ )
res += max(0LL, (long long int )(min(L[i], R[i]) - ar[i])*K*M);
printf("%lld\n", res);
return 0;
}
Special thanks to Burak Bugrul for the implementation of this question.
Question Five - Halil and The Party - O(N)
We need to count consecutive numbers in this question. If we have K consecutive numbers, Halil can not jump away from the numbers.
#include <utility>
#include <cmath>
#include <cstdio>
#include <utility>
#include <vector>
#include <iostream>
#include <climits>
#include <limits>
#include <algorithm>
#include <iostream>
#include <set>
#include <fstream>
#include <queue>
#include <bitset>
#include <map>
#include <stack>
#include <sstream>
#include <list>
using namespace std;
int main() {
int t;
cin >> t;
while (t-- > 0) {
int n,k;
cin >> n >> k;
string s;
cin >> s;
int counter = 0;
bool flag = true;
for (char i : s) {
// If we hit a non-number, we need to reset the counter.
if(i >= '0' && i <= '9') counter++;
else counter = 0;
// If consecutive numbers are greater than the value k, Halil will become offensive.
flag = flag & (counter < k);
if(!flag) break;
}
if(flag) cout << ":)" << endl;
else cout << ":(" << endl;
}
return 0;
}
Question Six - Blackbeard Rgzi - O(N•logN)
There are several ways to solve this question. One of those ways is divide and conquer approach. We need to count bigger elements, that has the smaller index and bigger value while merging our subarray. Therefore, we just need to count that condition while merging our subarray. Furthermore, do not forget to sort that subarrays like in mergesort.
#include <utility>
#include <cmath>
#include <cstdio>
#include <utility>
#include <vector>
#include <iostream>
#include <climits>
#include <limits>
#include <algorithm>
#include <iostream>
#include <set>
#include <fstream>
#include <queue>
#include <bitset>
#include <map>
#include <stack>
#include <sstream>
#include <list>
using namespace std;
long long sort_and_count(vector<long long>::iterator begin, vector<long long>::iterator end) {
if (end - begin <= 1)
return 0;
auto mid = begin + (end - begin) / 2;
long long count = sort_and_count(begin, mid) + sort_and_count(mid, end);
for (auto i = begin, j = mid; i != mid; ++i) {
while (j != end and *i > 2L * *j)
++j;
count += j - mid;
}
inplace_merge(begin, mid, end);
return count;
}
int reversePairs(vector<long long>& nums) {
return sort_and_count(nums.begin(), nums.end());
}
int main() {
int n;
cin >> n;
vector<long long> nums(n);
for(int i=0;i<n;i++) cin >> nums[i];
cout << reversePairs(nums)+1 << endl;
return 0;
}